POSTERIOR AGREEMENT FOR CONNECTIVITY-BASED CORTEX PARCELLATION

Author: Nico Stephan Gorbach , Institute of Machine Learning, ETHZ, email: nico.gorbach@inf.ethz.ch

Implementation of " Pipeline Validation for Connectivity-based Cortex Parcellation " by Nico S. Gorbach, Marc Tittgemeyer and Joachim M. Buhmann. The doctoral thesis https://www.research-collection.ethz.ch/handle/20.500.11850/261734 describes this algorithm in more detail.

Contents

clear all; close all

Introduction

This instuctional code demonstrates validation by posterior agreement for connectivity-based cortex parcellation of diffusion weighted imaging data. We assume that a connectivity matrix is given. In particular, we validate histogram clustering. Additionally, we provide the option of validating smooth histogram clustering (by setting smooth_clustering=true in the input) which adds a spatial regularity to the seed voxels.

Input

path.connectivity_matrix = './5203/neighbourhood_tracking/45_directions/connectivity_matrix.mat';    % path to connectivity matrix
path.seed_coords = './5203/neighbourhood_tracking/45_directions/seed_coords.txt';                    % path to seed coordinates
path.results_directory = './5203/neighbourhood_tracking/45_directions/';                             % directory to save results
K = 2:3:29;                                                     % number of potential clusters (vector of integers)

% Smooth histogram clustering
smooth_clustering = false;                                    % perform standard histogram clustering or smooth histogram clustering (Boolean)
smooth_weighting = 10;                                        % weight of the smoothness penalty (real positive number)
number_of_neighbours = 80;                                    % number of neighbours %20,50,80

Imports

connectivity_matrix = importdata(path.connectivity_matrix);
seed_coords = importdata(path.seed_coords);

Distance between connectivity matrices

seed_idx = randperm(size(connectivity_matrix{1},1)); seed_idx = sort(seed_idx(1:1000));
p = bsxfun(@rdivide,connectivity_matrix{1}(seed_idx,:),sum(connectivity_matrix{1}(seed_idx,:),2));
q = bsxfun(@rdivide,connectivity_matrix{2}(seed_idx,:),sum(connectivity_matrix{2}(seed_idx,:),2));
for i = 1:size(p,1)
    dsim_across_instances.JSDiv(i) = JSDiv(p(i,:),q(i,:));
    dsim_across_instances.euclid(i) = pdist2(p(i,:),q(i,:));
    dsim_across_instances.hamming = pdist2(double(logical(p(i,:))),double(logical(q(i,:))),'hamming');
end

disp(['Average Jenson Shannon distance between connectivity matrices: ' num2str(mean(dsim_across_instances.JSDiv))]);
disp(['Average Euclidean distance between connectivity matrices: ' num2str(mean(dsim_across_instances.euclid))]);
disp(['Average Hamming distance between connectivity matrices: ' num2str(mean(dsim_across_instances.hamming))]);
%

Average Jenson Shannon distance between connectivity matrices: 0.54531
Average Euclidean distance between connectivity matrices: 0.066218
Average Hamming distance between connectivity matrices: 0.012698

Nearest neighbours for smooth histogram clustering

if smooth_clustering
    dsim_seed_coords = pdist2(seed_coords,seed_coords);
    dsim_seed_coords(logical(eye(size(dsim_seed_coords,1)))) = realmax;
    [nearest_neighbours.dist,nearest_neighbours.idx] = sort(dsim_seed_coords,2,'ascend');
    nearest_neighbours.dist = nearest_neighbours.dist(:,1:number_of_neighbours);
    nearest_neighbours.idx = nearest_neighbours.idx(:,1:number_of_neighbours);
end

% remove zero columns
rm_idx(1,:) = sum(connectivity_matrix{1},1)==0;
rm_idx(2,:) = sum(connectivity_matrix{2},1)==0;
connectivity_matrix{1}(:,rm_idx(1,:)) = [];
connectivity_matrix{2}(:,rm_idx(2,:)) = [];

% dissimilarity matrix
if exist([path.results_directory 'dsim.mat1'])
    dsim = importdata([path.results_directory 'dsim.mat']);
else
    %d = connectivity_matrix{1}; d(:,sum(d,1)<4000) = [];
    d = connectivity_matrix{1}; d(:,sum(d,1)<600) = []; d = single(full(d));
    dsim = pdist2(d,d);
%     d = bsxfun(@rdivide,d,sum(d,2));
%     log_d = d; log_d(log_d==0) = eps; log_d = log(log_d);
%     dsim = single(full(-d * log_d'));
%     dsim = flipdim(flipdim((dsim + dsim') / 2,1),2);
%     dsim(logical(eye(size(dsim,1)))) = mean(mean(dsim));
%     save([path.results_directory 'dsim.mat'],'dsim','-v7.3');
%     clear d log_d
end

% preprocessing for Bayesian evidence

alpha{1} = full(sum(connectivity_matrix{1},1));
alpha{2} = full(sum(connectivity_matrix{1},1))/100;

% start timer
tic;

Deterministic annealing

Determine global minimizer.

% Annealing settings
inv_temp_init = 1/1000;                 % starting inverse temperature (5000 for smooth hc)
inv_temp_step = 1.1;                    % inverse temperature step
inv_temp_stop = 1/10;                   % stopping inverse temperature
perturb_sd = 1e-6;                      % centroid perturbation

for k = K

    % Initialization of Gibbs distributions
    gibbs_dist1 = ones(size(connectivity_matrix{1},1),k) ./ k;
    gibbs_dist2 = ones(size(connectivity_matrix{2},1),k) ./ k;

    % Initialization of centroids
    centroids1 = gibbs_dist1'*connectivity_matrix{1};
    centroids1 = bsxfun(@rdivide,centroids1,sum(centroids1,2));
    centroids1(centroids1==0) = eps;
    centroids2 = gibbs_dist2'*connectivity_matrix{2};
    centroids2 = bsxfun(@rdivide,centroids2,sum(centroids2,2));
    centroids2(centroids2==0) = eps;

    j = 0; inv_temp = inv_temp_init; inv_temp_pack = []; %subplot(2,2,3); cla
    while inv_temp <= inv_temp_stop

Perturb centroids

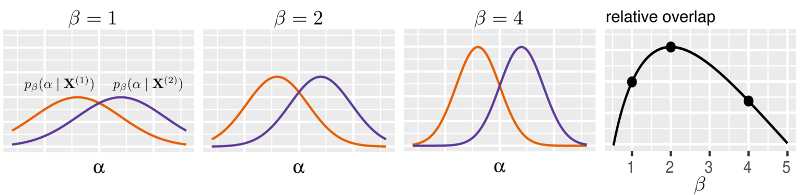
Avoid local minimum by perturbing centroids: 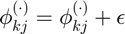$\phi_{kj}^{(\cdot)} = \phi_{kj}^{(\cdot)} + \epsilon$

        centroids1 = centroids1 + perturb_sd * rand(size(centroids1));
        centroids1 = bsxfun(@rdivide,centroids1,sum(centroids1,2)); % normalize
        centroids2 = centroids2 + perturb_sd * rand(size(centroids2));
        centroids2 = bsxfun(@rdivide,centroids2,sum(centroids2,2)); % normalize

Expectation maximization

Iterate between determining Gibbs distributions and maximzing variational lower bound w.r.t. centroids.

        for iter = 1:10

Costs for histogram clustering given instance 1

KL divergence between empirical probabilities (data) and centroid probabilities (up to proportionality constant): 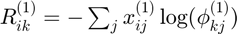$R_{ik}^{(1)} = -\sum_{j} x_{ij}^{(1)} \log(\phi_{kj}^{(1)})$

            potential1 = -connectivity_matrix{1} * log(centroids1)';

Costs for histogram clustering given instance 2

KL divergence between empirical probabilities (data) and centroid probabilities (up to proportionality constant): 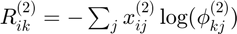$R_{ik}^{(2)} = -\sum_{j} x_{ij}^{(2)} \log(\phi_{kj}^{(2)})$

            potential2 = -connectivity_matrix{2} * log(centroids2)';

Smoothness potential

            if smooth_clustering
                smooth_potential1 = blockfun(1-gibbs_dist1(nearest_neighbours.idx',:),...
                    [size(nearest_neighbours.idx,2),1],@sum);

                smooth_potential2 = blockfun(1-gibbs_dist2(nearest_neighbours.idx',:),...
                    [size(nearest_neighbours.idx,2),1],@sum);

                potential1 = potential1 + smooth_weighting * smooth_potential1;
                potential2 = potential2 + smooth_weighting * smooth_potential2;
            end

Gibbs distribution 1

Maximum entropy distribution: 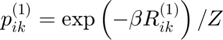$p_{ik}^{(1)} = \exp \left( -\beta R_{ik}^{(1)} \right) / Z$

            gibbs_dist1 = exp(-inv_temp * potential1);
            partition_sum1 = sum(gibbs_dist1,2);
            gibbs_dist1 = bsxfun(@rdivide,gibbs_dist1,partition_sum1);

            % avoid underflow
            idx = find(partition_sum1==0);
            if ~isempty(idx)
                [~,min_cost_idx] = min(potential1(idx,:),[],2);
                max_ind = sub2ind(size(gibbs_dist1),idx,min_cost_idx);
                gibbs_dist1(idx,:) = zeros(length(idx),k);
                gibbs_dist1(max_ind) = 1;
            end

Gibbs distribution 2

Maximum entropy distribution: 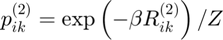$p_{ik}^{(2)} = \exp \left(-\beta R_{ik}^{(2)} \right) / Z$

            gibbs_dist2 = exp(-inv_temp * potential2);
            partition_sum2 = sum(gibbs_dist2,2);
            gibbs_dist2 = bsxfun(@rdivide,gibbs_dist2,partition_sum2);

            % avoid underflow
            idx = find(partition_sum2==0);
            if ~isempty(idx)
                [~,min_cost_idx] = min(potential2(idx,:),[],2);
                max_ind = sub2ind(size(gibbs_dist2),idx,min_cost_idx);
                gibbs_dist2(idx,:) = zeros(length(idx),k);
                gibbs_dist2(max_ind) = 1;
            end

Joint Gibbs distribution

Maximum entropy distribution: 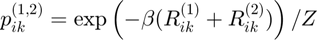$p_{ik}^{(1,2)} = \exp \left(-\beta ( R_{ik}^{(1)} + R_{ik}^{(2)}) \right) / Z$

            dist_joint = exp(-inv_temp * (potential1 + potential2));
            joint_partition_sum = sum(dist_joint,2);

Centroids for instance 1

Probability prototype: 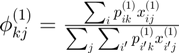$\phi_{kj}^{(1)} = \frac{\sum_i p_{ik}^{(1)} x_{ij}^{(1)}}{\sum_j \sum_{i'} p_{i'k}^{(1)} x_{i'j}^{(1)}}$

            centroids1 = gibbs_dist1'*connectivity_matrix{1};
            centroids1 = bsxfun(@rdivide,centroids1,sum(centroids1,2));
            centroids1(centroids1==0) = eps;

Centroids for instance 2

Probability prototype: 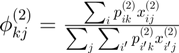$\phi_{kj}^{(2)} = \frac{\sum_i p_{ik}^{(2)} x_{ij}^{(2)}}{\sum_j \sum_{i'} p_{i'k}^{(2)} x_{i'j}^{(2)}}$

            centroids2 = gibbs_dist2'*connectivity_matrix{2};
            centroids2 = bsxfun(@rdivide,centroids2,sum(centroids2,2));
            centroids2(centroids2==0) = eps;
        end

        % increase inverse temperature:
        inv_temp = inv_temp * inv_temp_step;

Match clusters across data instances

Use Hungarian algorithm to match clusters.

        c1 = zeros(k,length(rm_idx(1,:))); c2 = zeros(k,length(rm_idx(2,:)));
        c1(:,~rm_idx(1,:)) = centroids1; c2(:,~rm_idx(2,:)) = centroids2;
        match_clusters_idx = munkres(pdist2(c1,c2));
        potential2=potential2(:,match_clusters_idx);

Log partition sum for instance 1

Determine log partition sum while avoiding underflow: 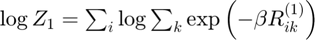$\log Z_1 = \sum_i \log \sum_k \exp \left( -\beta R_{ik}^{(1)} \right)$

        scaled_cost1 = -inv_temp * potential1;
        % log-sum-exp trick to prevent underflow
        max_scaled_cost1 = max(scaled_cost1,[],2);
        log_partition_sum1 = max_scaled_cost1 + log(sum(exp(bsxfun(@minus,scaled_cost1,max_scaled_cost1)),2));

Log partition sum for instance 2

Determine log partition sum while avoiding underflow: 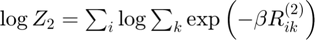$\log Z_2 = \sum_i \log \sum_k \exp \left( -\beta R_{ik}^{(2)} \right)$

        scaled_cost2 = -inv_temp * potential2;
        % log-sum-exp trick to prevent underflow
        max_scaled_cost2 = max(scaled_cost2,[],2);
        log_partition_sum2 = max_scaled_cost2 + log(sum(exp(bsxfun(@minus,scaled_cost2,max_scaled_cost2)),2));

Joint log partition sum

Determine joint log partition sum while avoiding underflow: 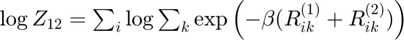$\log Z_{12} = \sum_i \log \sum_k \exp \left( -\beta ( R_{ik}^{(1)} + R_{ik}^{(2)} ) \right)$

        joint_scaled_cost = -inv_temp * (potential1 + potential2);
        % log-sum-exp trick to prevent underflow
        max_scaled_cost3 = max(joint_scaled_cost,[],2);
        log_joint_partition_sum = max_scaled_cost3 + log(sum(exp(bsxfun(@minus,joint_scaled_cost,max_scaled_cost3)),2));

        j = j+1;

Generalization capacity

Resolution of the hypothesis space: 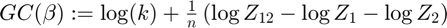$GC(\beta) := \log(k) + \frac{1}{n} \left( \log Z_{12} - \log Z_1 - \log Z_2 \right)$

        gc{k}(j) = log(k) + sum(log_joint_partition_sum - log_partition_sum1 ...
            - log_partition_sum2) ./ size(partition_sum1,1);

        % pack
        inv_temp_pack(j) = inv_temp;
        gibbs_dist_packed1{k}(:,:,j) = single(gibbs_dist1);
        gibbs_dist_packed2{k}(:,:,j) = single(gibbs_dist2(:,match_clusters_idx));

%         gc_plot = gc{k}; %gc_plot(gc_plot<0) = NaN;
%         hold on; plot(inv_temp,gc_plot,'LineWidth',2); drawnow

    end

Number of equivariant transformations

Richness of the hypothesis space: 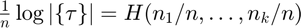$\frac{1}{n} \log|\{\tau\}| = H(n_1/n,\ldots,n_k/n)$

    gibbs_dist1 = round(gibbs_dist1);
    d = sum(gibbs_dist1,1); d = d./sum(d); d(d==0) = 1;
    nTransformations = -d * log(d)';

    % correct generalization capacity
    gc{k} = gc{k}-log(k)+nTransformations;

    % transforming units from nats to bits
    gc{k} = gc{k} * log2(exp(1));

Information content (ASC)

Quality of algorithm: 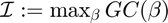$\mathcal{I} := \max_{\beta} GC(\beta)$

    [info_content(k),max_gc_idx(k)] = max(gc{k});

Bayesian Information Criterion (BIC)

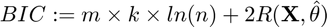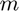$BIC := m \times k \times ln (n) + 2 R(\mathbf{X},\hat{\theta})$ where $m$ is the number of bins and 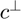$c^{\perp}$ is the empirical risk minimizer

    if ~smooth_clustering
        cost = sum(sum(gibbs_dist1 .* (-connectivity_matrix{1} * log(centroids1)')));
    else
        cost = sum(sum(potential1(logical(gibbs_dist1))));
    end
    BIC(k) = size(connectivity_matrix{1},2) * k * log(size(connectivity_matrix{1},1)) + 2 * cost;

Akaike Information Criterion (AIC)

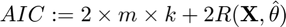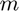$AIC := 2 \times m \times k + 2 R(\mathbf{X},\hat{\theta})$ where $m$ is the number of bins and 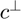$c^{\perp}$ is the empirical risk minimizer

    AIC(k) = 2 * size(connectivity_matrix{1},2) * k + 2 * cost;

Bayesian evidence

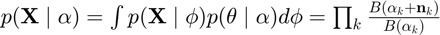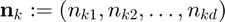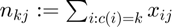
$p(\mathbf{X} \mid \alpha) = \int p(\mathbf{X} \mid \phi) p(\theta \mid \alpha) d\phi = \prod_k \frac{B(\alpha_k + \mathbf{n}_k)}{B(\alpha_k)}$ where $\mathbf{n}_k := (n_{k1},n_{k2},\ldots,n_{kd})$ and $n_{kj} := \sum_{i:c(i)=k} x_{ij}$

    [~,labels] = max(gibbs_dist1,[],2);
    log_bayes_evidence{1}(k) = 0;
    log_bayes_evidence{2}(k) = 0;
    for c = unique(labels)'
        ncj = full(sum(connectivity_matrix{1}(labels==c,:),1));
        alpha_tmp{1} = alpha{1}/k; alpha_tmp{1}(ncj==0) = [];
        alpha_tmp{2} = alpha{2}; alpha_tmp{2}(ncj==0) = [];
        ncj(ncj==0) = [];

        log_bayes_evidence{1}(k) = log_bayes_evidence{1}(k) + sum(gammaln(alpha_tmp{1} + ncj)) ...
            + gammaln(sum(alpha_tmp{1})) - gammaln(sum(alpha_tmp{1} + ncj)) - sum(gammaln(alpha_tmp{1}));
        log_bayes_evidence{2}(k) = log_bayes_evidence{2}(k) + sum(gammaln(alpha_tmp{2} + ncj)) ...
            + gammaln(sum(alpha_tmp{2})) - gammaln(sum(alpha_tmp{2} + ncj)) - sum(gammaln(alpha_tmp{2}));
    end

Number of misclustered seed voxels

    number_misclustered_objects(k) = sum(diag(round(gibbs_dist1)' * ~round(gibbs_dist2(:,match_clusters_idx))))/2;

Distance between centroids

    [~,max_gc_idx] = max(gc{k});
    centroids_opt = double(gibbs_dist_packed1{k}(:,:,max_gc_idx))'*connectivity_matrix{1};
    centroids_opt = bsxfun(@rdivide,centroids_opt,sum(centroids_opt,2));
    centroids_opt(centroids_opt==0) = eps;

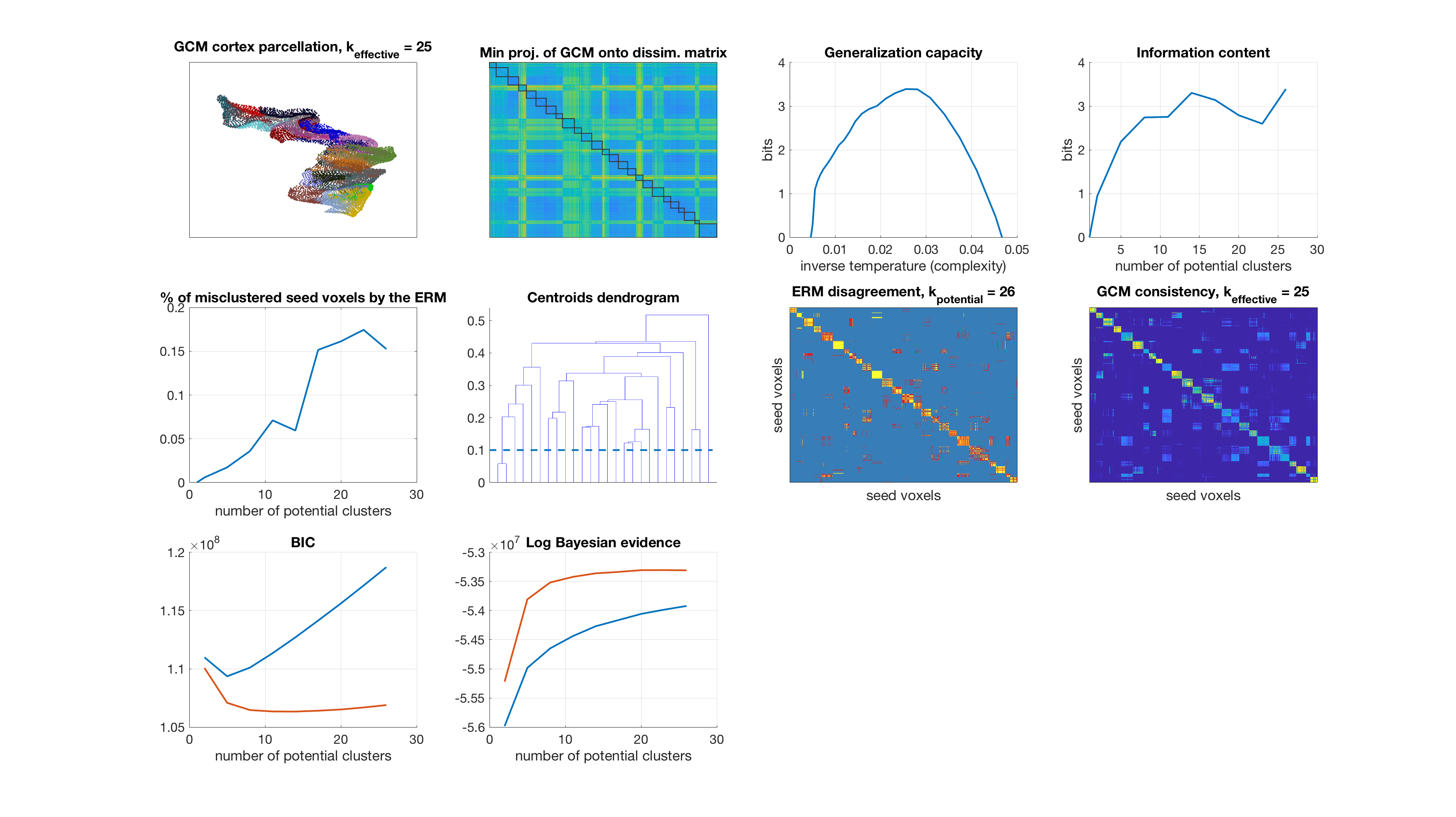
Results

    display_result(gc,info_content,gibbs_dist_packed1,gibbs_dist_packed2,inv_temp_pack,log_bayes_evidence,BIC,AIC,K(1:find(K==k)),...
        dsim,centroids_opt,number_misclustered_objects,seed_coords);

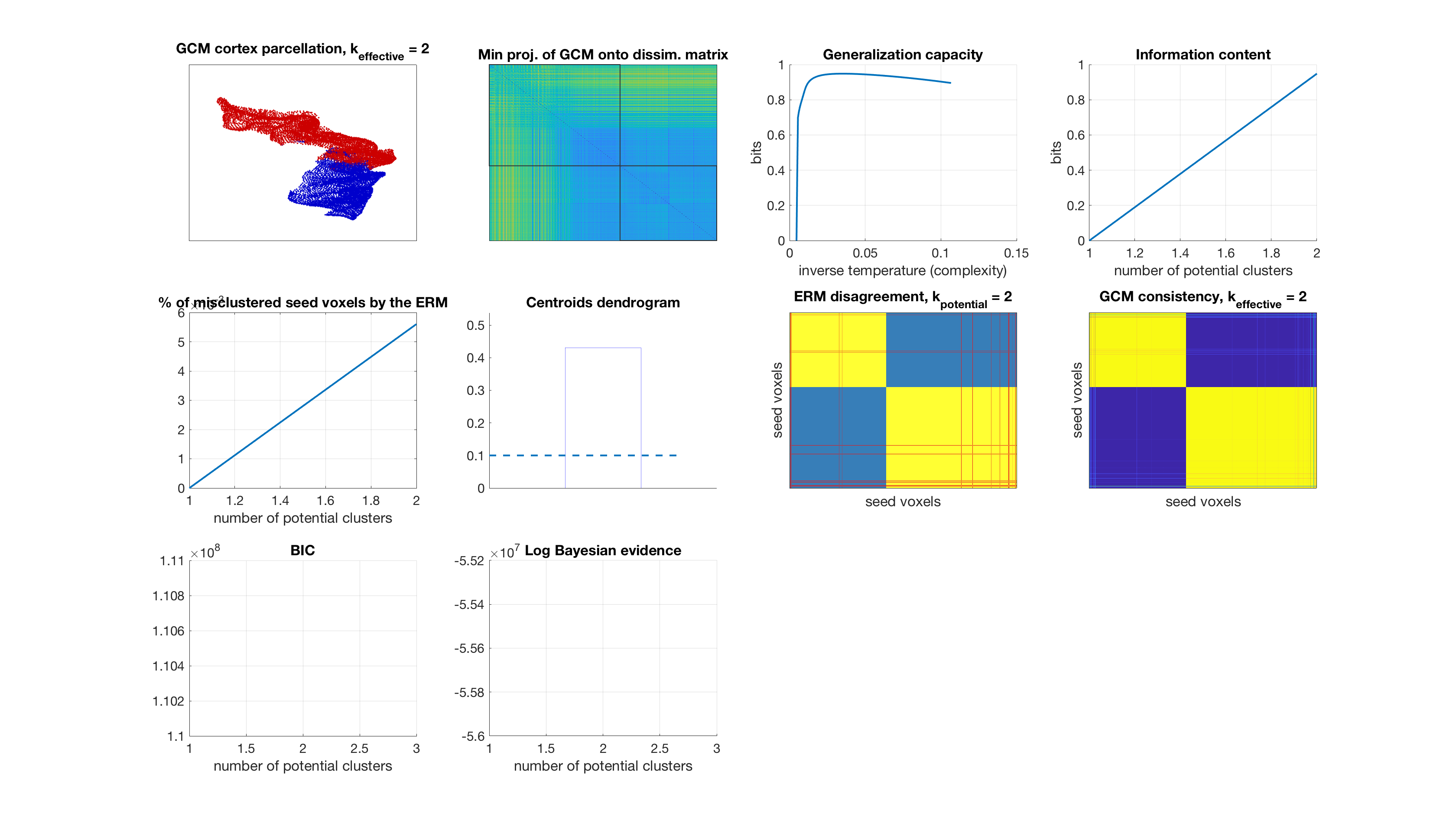
Number of potential clusters: 2

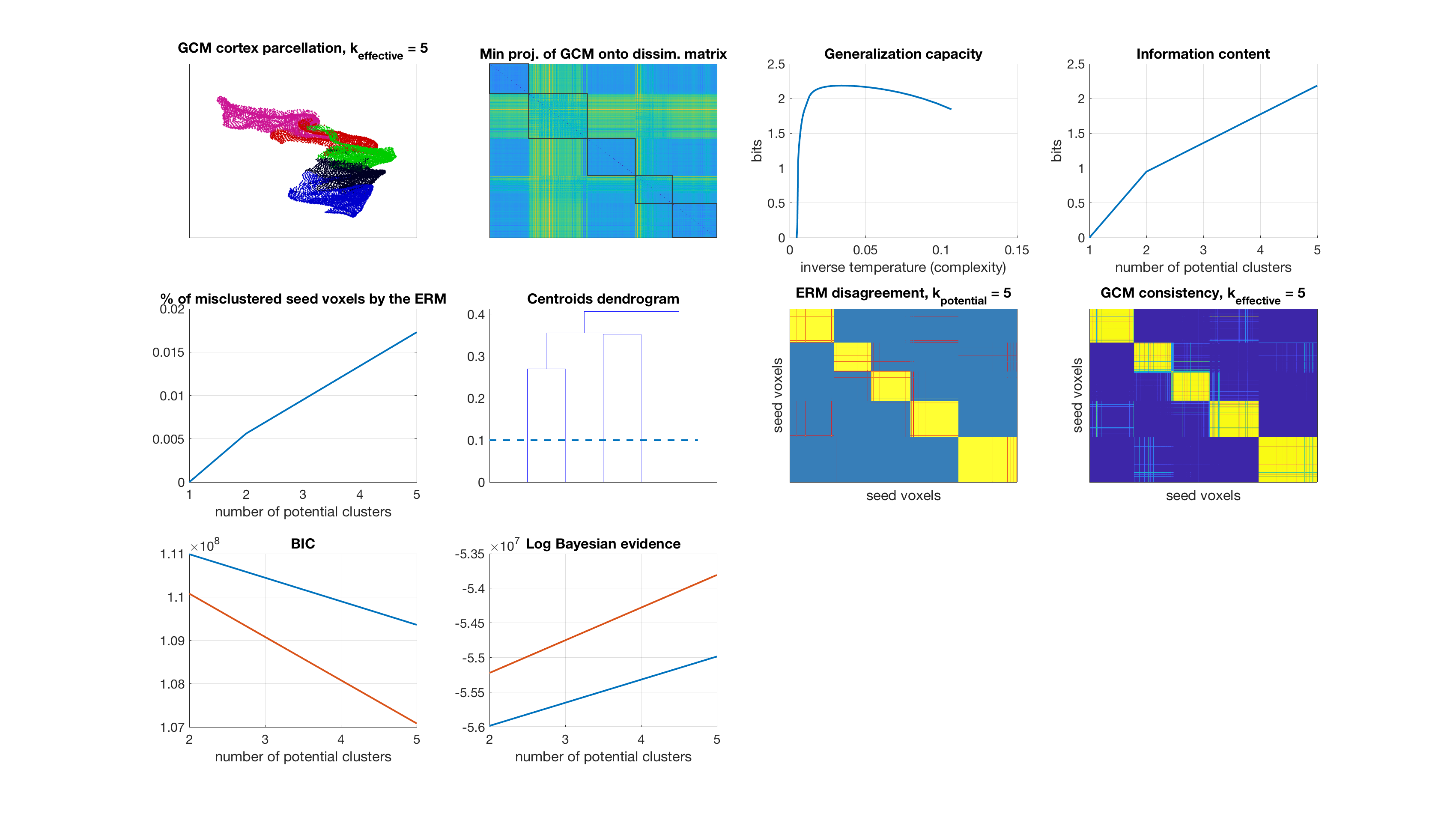
Number of potential clusters: 5

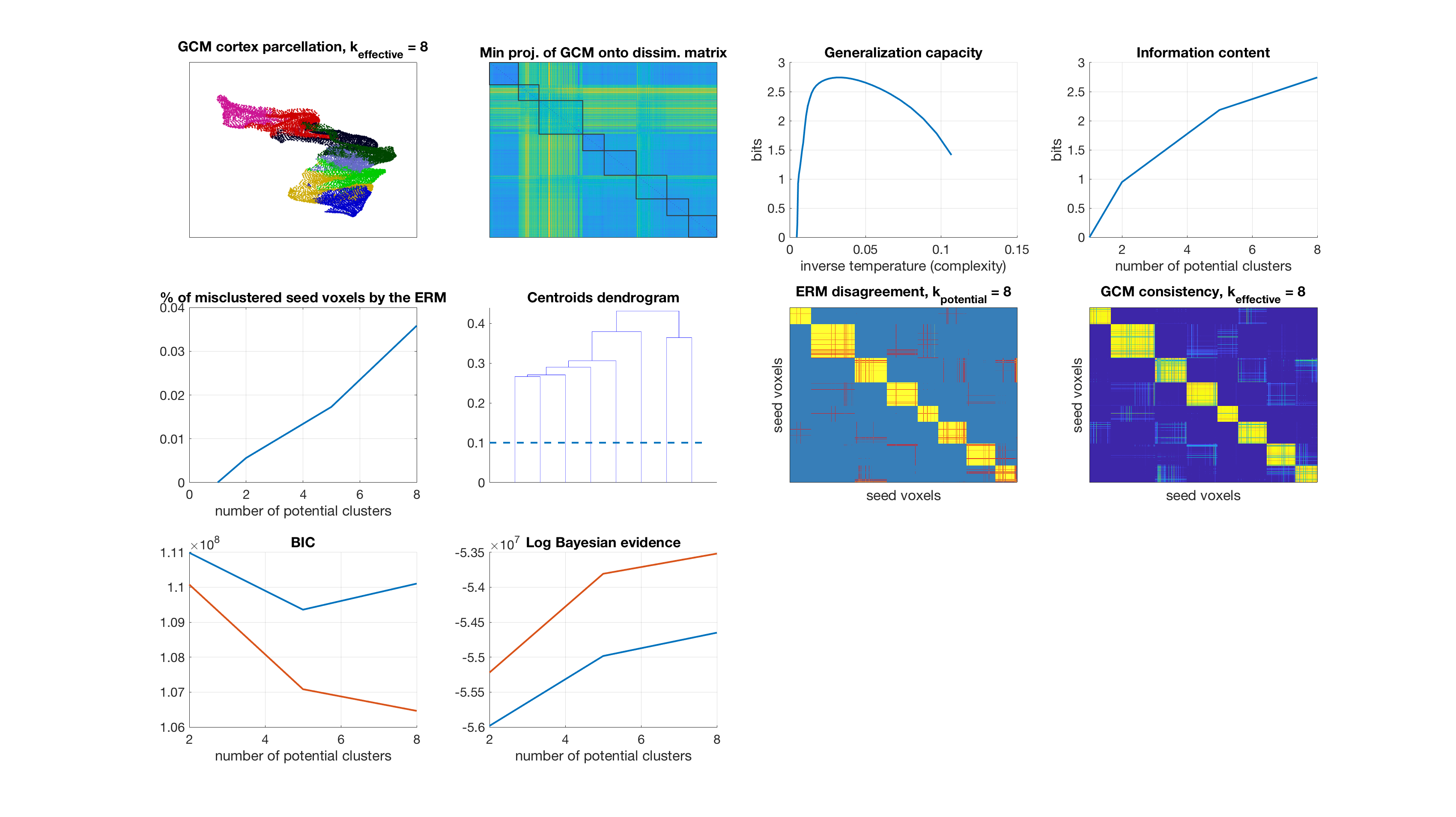
Number of potential clusters: 8

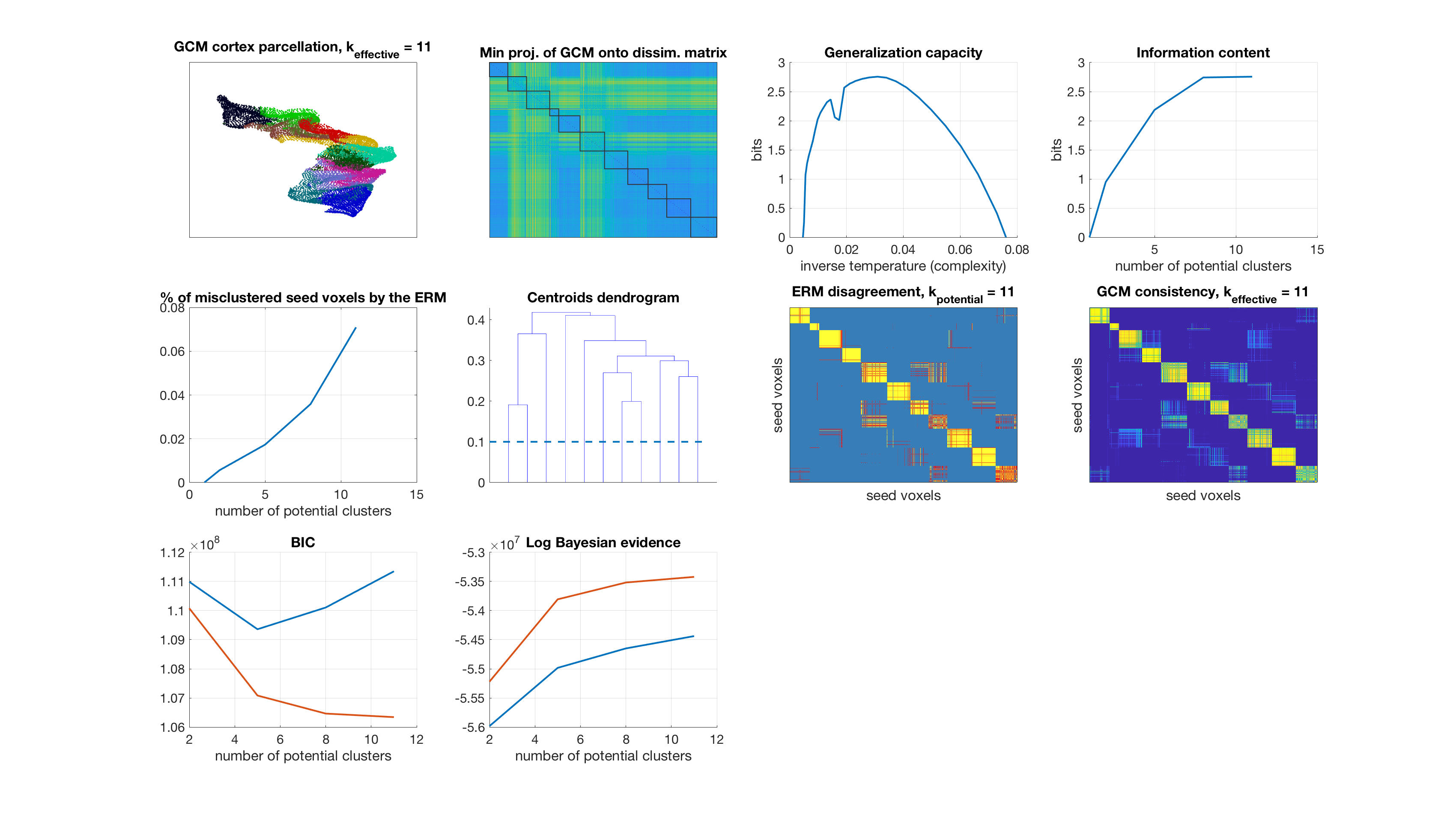
Number of potential clusters: 11

Number of potential clusters: 14

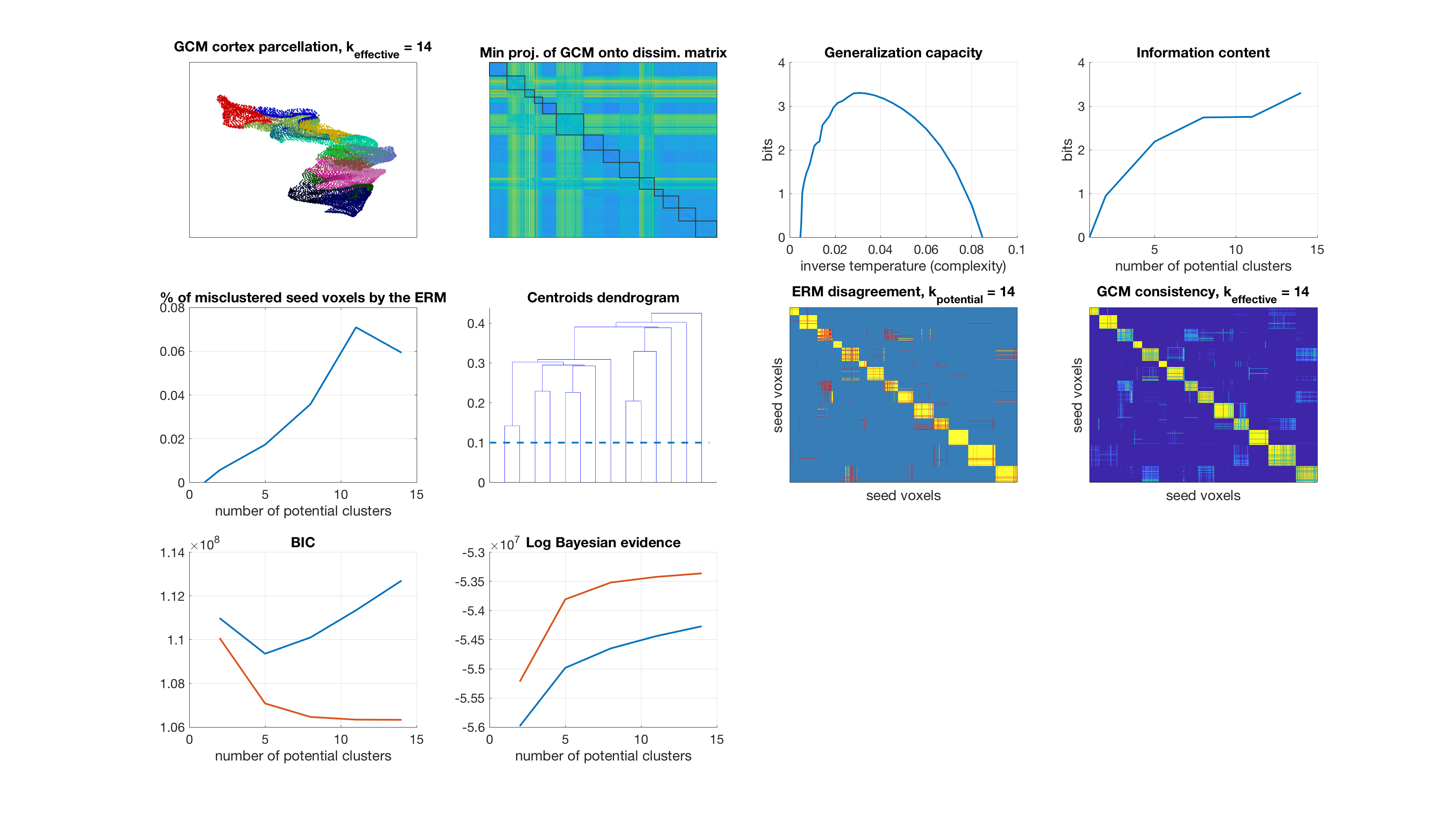
Number of potential clusters: 17

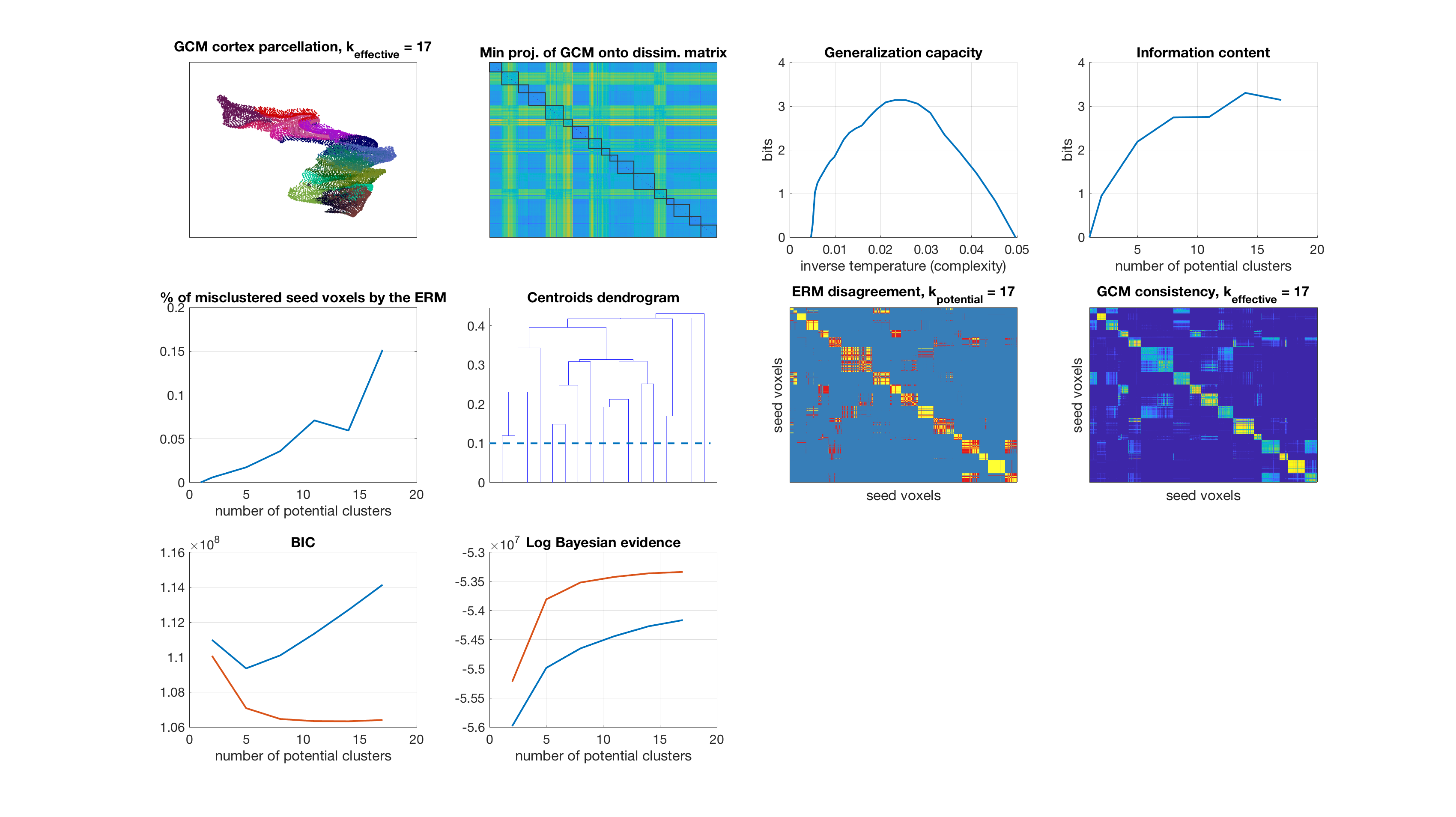
Number of potential clusters: 20

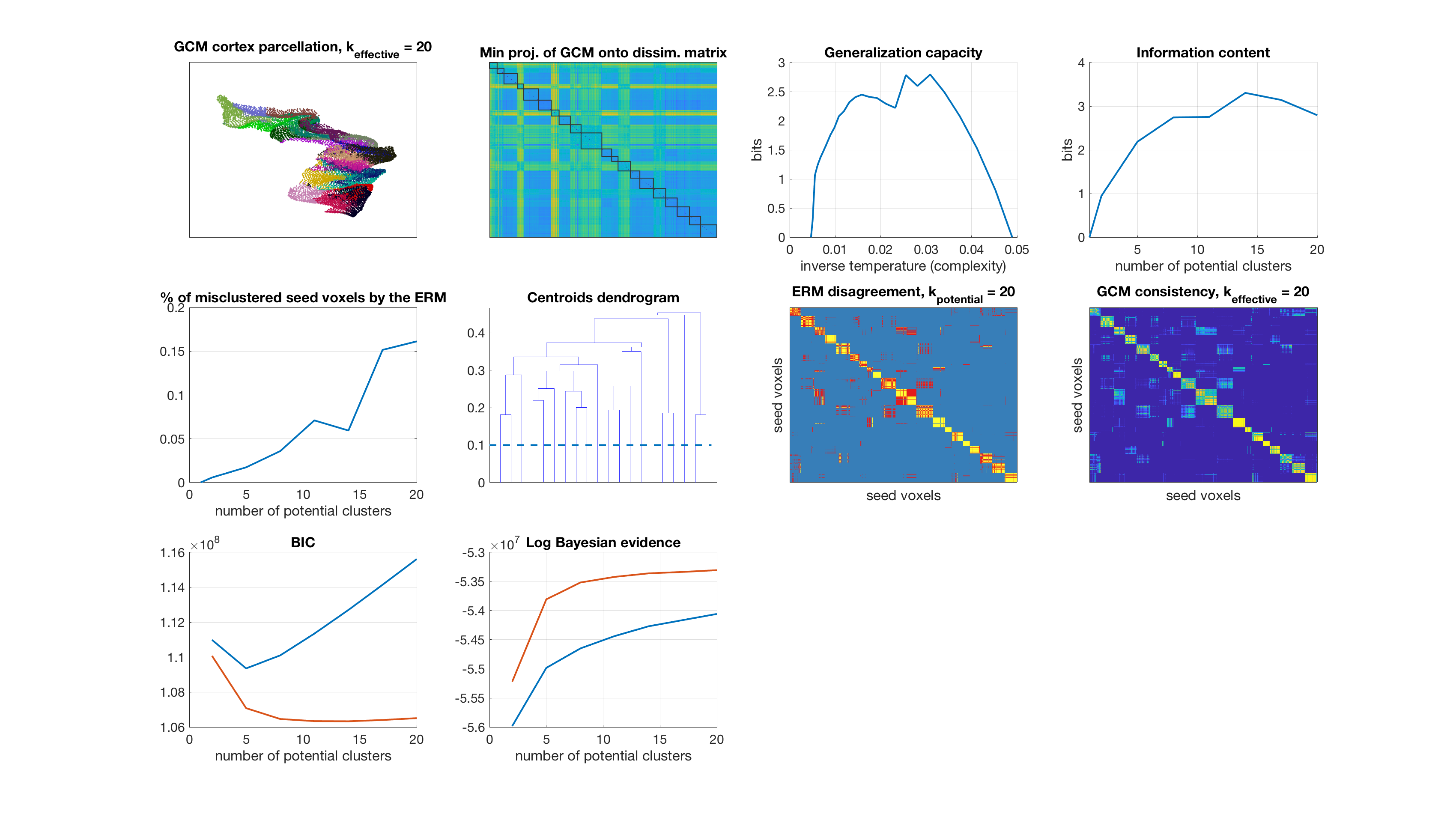
Number of potential clusters: 23

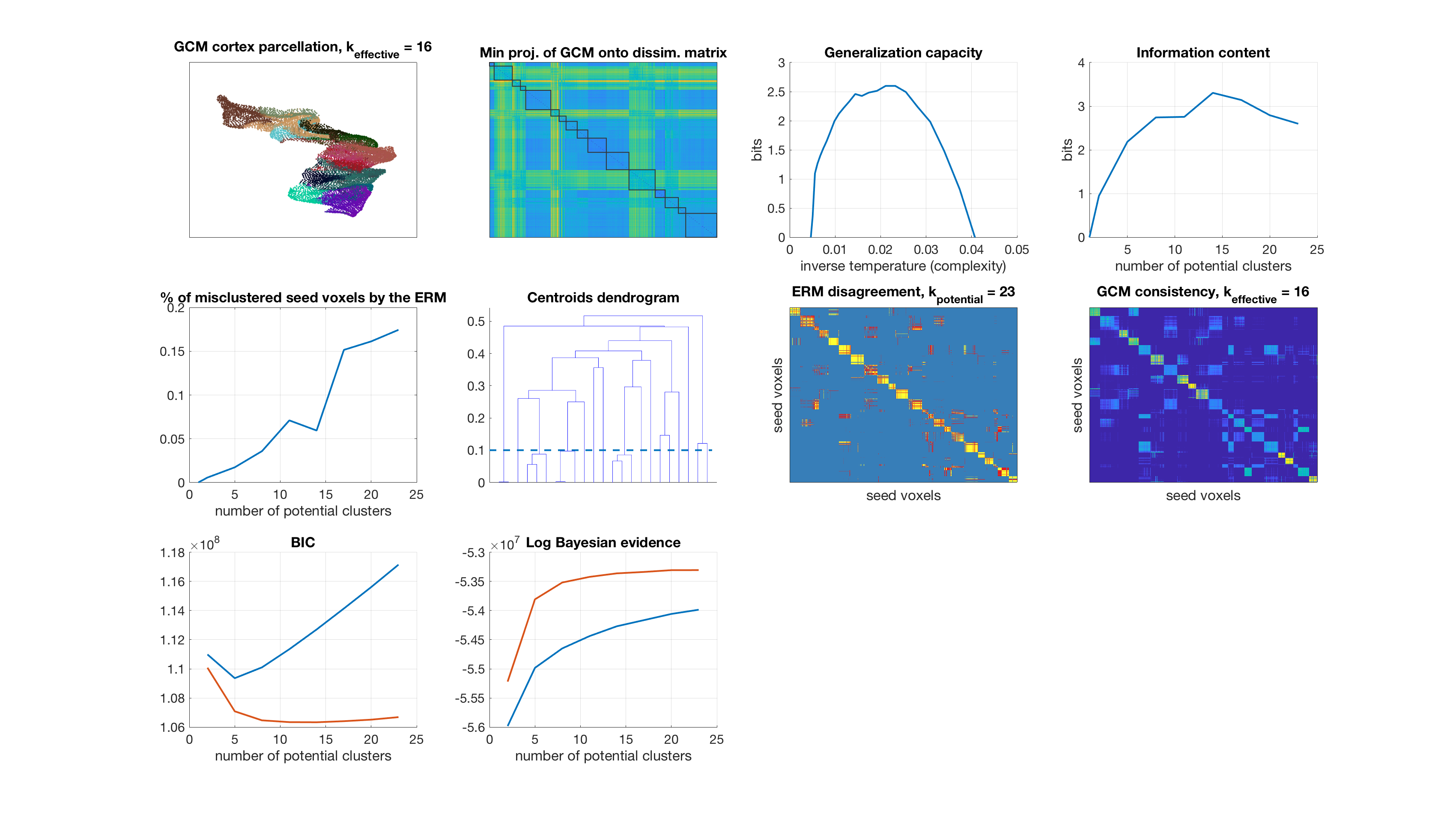
Number of potential clusters: 26

Number of potential clusters: 29

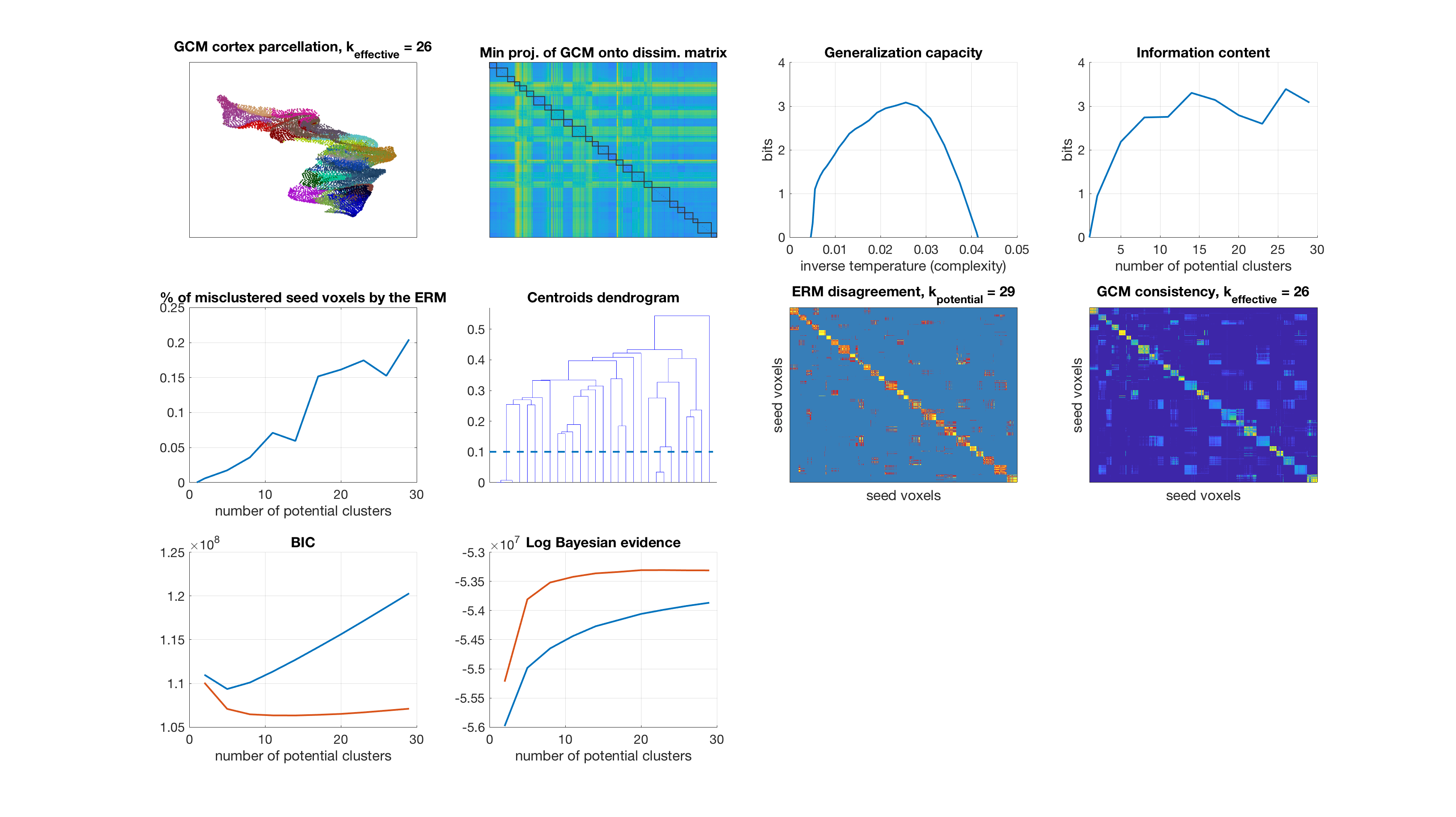
end

Runtime

% display runtime
disp(['runtime: ' num2str(toc/60) ' minutes on ' computer])

runtime: 28.6007 minutes on MACI64

% save resutls
%save([path.results_directory 'parcellation.mat'],'gibbs_dist_packed1','gibbs_dist_packed2','gc','info_content','BIC','AIC','log_bayes_evidence','dsim_across_instances')
save([path.results_directory 'parcellation.mat'],'gibbs_dist_packed1','gibbs_dist_packed2','gc','info_content','BIC','AIC','log_bayes_evidence')

Video


Published with MATLAB® R2017a